2. One dimensional Monte Carlo Integration.

Ref.: S. E. Koonin and D. C. Meredith, Computational Physics (1990; out of print).

Use Monte Carlo methods (random point sampling) to do the integral

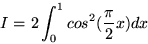$$I = 2 \int_0^1 cos^2(\frac{\pi}{2}x) dx$$ (5)

in two ways.
$\bullet$ simply and naively, with weight function w(x) = 1. Also, accumulate the uncertainty.
$\bullet$ with importance sampling, using the weight function

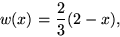$$w(x) = \frac{2}{3}(2-x),$$ (6)

which is non-negative, is normalized properly (average is unity) and weights smaller values of x more heavily than larger values in the interval (0,1).

N.B. When you calculate

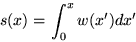$$s(x) = \int_0^x w(x^{\prime}) dx^{\prime}$$ (7)

and invert to get  x(s), be sure to choose the correct root.

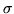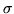Use N points for both integrals, with N = 10, 30, 100, 300, 1000, 3000, 10000. Write out the error (relative to the exact analytic value) in columnar form to facilitate easy comparison of the accuracy of the two methods. Write out also the statistical uncertainty $\sigma$ for each calculation, and check whether the answer is within $\sigma$ of the correct answer.