1. Discrete Numerical Derivatives.

Use the various forms for the numerical first derivative for a uniform discrete mesh size h:

1.

the 3-point formula

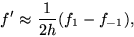$$f^{\prime} \approx \frac{1}{2h}(f_1 - f_{-1}),$$ (1)

2.

the forward and backward 4-point formulas

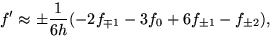$$f^{\prime} \approx \pm \frac{1}{6h}(-2f_{\mp 1}-3f_0 +6f_{\pm 1} -f_{\pm2}),$$ (2)

3.

the 5-point formula

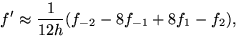$$f^{\prime} \approx \frac{1}{12h}(f_{-2} - 8f_{-1} +8f_1 -f_{2}),$$ (3)

to evaluate the derivative

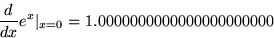$$\frac{d}{dx}e^x\vert _{x=0} = 1.0000000000000000000000$$ (4)

Use the quasi-logarithmic values for h = 1., 0.3, 0.1, 0.03, 0.01, ... 10^-6. Use double precision and print out in scientific notation the error (i.e. subtract 1.d0) with 14 significant figures shown (not that the last one or two will be significant). Print them out in a columnar table so the rates of convergence will we easy to see.